Геогебра как пользоваться

GeoGebra на русском

GeoGebra (Геогебра) — бесплатное ПО по математике, которое объединяет геометрию, алгебру и математический анализ. Интерфейс программы очень прост, однако имеет мощные функции для создания конструкций точек, векторов, отрезков, прямых, многоугольников и конических сечений, а также функций и их динамических изменений.

Полное описание программы GeoGebra

GeoGebra может работать с переменными чисел, векторов и точек, находить производные и интегралы от функций и предлагает такие команды, как Корень или Вершина.

С помощью предоставленных инструментов геометрии в панели инструментов вы можете создавать геометрические построения с помощью мыши или напрямую ввести алгебраические данные, команды и функции в строке ввода. Скачать GeoGebra, гибкий интерфейс имеет несколько видов конфигурации: Графики и Алгебры, вид Электронной таблицы, Компьютерной Алгебры (ВКА), а также Графической вид.

Основные функции GeoGebra

— Геометрические построения, вычисления, анализ. — Создание чертежей. — Рисование изображений.

Название приложения:Автор/Разработчик:Версия/сборка:Дата обновления: Размер скачиваемого файла:Операционная система:Наличие русского языка:Распространяется:

GeoGebrawww.geogebra.org 6.0.587.0 2020-05-29 60 МБ Windows 10, 8, 7, Vista, XP русскийбесплатно (Free)

Скачать GeoGebra

• Безопасность
  • Антивирусы
  • Обновление баз
  • Файерволы
  • Сканеры
  • Антиспам
  • Антишпионы
  • Загрузочные CD
  • Шифрование. Пароли. Доступ
  • Дополнительная защита
• Система
  • Восстановление
  • Очистка
  • Реестр
  • Деинсталляция
  • Дефрагментация
  • Драйверы
  • Настройка. Автозагрузка
  • Работа с разделами
  • Синхронизация
  • Файл-менеджеры
  • Архиваторы
  • Системные утилиты
• Интернет
  • Браузеры
  • Общение. Почта
  • Скачивание
  • Удалённый доступ
  • Вебмастеру
  • Rss ленты
  • Прочее для Интернет
• Мультимедиа
  • Кодеки
  • Конвертеры
  • Плееры
  • ТВ плееры
  • Радио
  • Редакторы Медиа
  • Захват аудио
  • Микшеры. Синтезаторы
  • Коллекции
  • Скриншот. Запись видео
  • Медиа программы
• Графика
  • Графические Редакторы
  • Просмотр
  • 3D моделирование
  • Прочие графические программы
• CD/DVD диски
  • Запись дисков
  • Эмуляторы
  • Работа с дисками
• Офис
  • Текстовые Редакторы
  • Переводчики
• Обучение. Учёба
  • Программирование
  • Музыка
  • Рисование
  • Математика
• Программы для игр
  • Аддоны World of Warcraft
  • Игровые магазины

• Плееры

файловый менеджер для Windows, бесплатный аналог Total Commander, имеет две панели с выбором тем оформления интерфейса, огромные функциональные возможности.

2020-04-29 HD VideoBox для Андроид

популярный онлайн каталог для Android, который предлагает к просмотру на смартфоне или планшете тысячи фильмов, сериалов, мультиков, телепередач и прочего видео контента.

2020-04-16 Kristal Audio Engine

бесплатная цифровая рабочая станция для записи, редактирования и воспроизведения звука. Совмещает многодорожечный рекордер, аудио секвенсор и микшер.

2020-04-10 PDF24 Creator

бесплатная программа для просмотра, создания и конвертирования электронных документов формата PDF в ос windows.

Будем рады видеть Вас в наших группах!

Контакты | Пользовательское соглашениеВнимание! Находясь на данном сайте, вы подтверждаете свое согласие на сбор метаданных. Сайт создан в 2011

Все права защищены.

Панель инструментов

Геогебра предоставляет широкий спектр инструментов для графического представления объектов. Перечислим их в том же порядке, в котором расположены иконки.

Перемещение, фигура от руки

Пример. Введем функцию f(x) = x³ — 2x² в поле ввода текста; сразу же будет отображен график функции. Введем команду производная . Снимем галочку «Закрепить объект» в свойствах этой кривой. Выберем режим «Перемещение». Будем перемещать график с помощью мыши и наблюдать за изменением уравнения функции и ее производной.

Фигура от руки и карандаш:

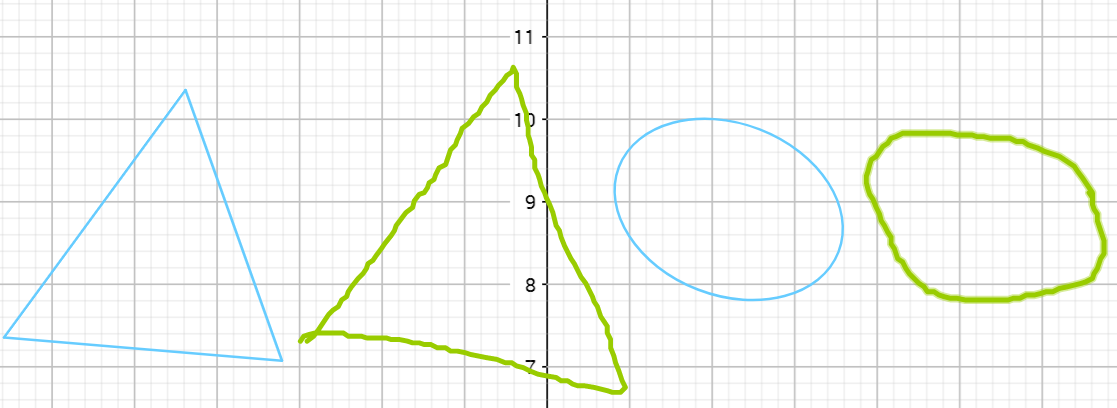
Точка, пересечение, середина отрезка

Группа инструментов под названием Точка:

Команда:Команда:

Примеры: Point[] — нарисовать точку с координатами (1,2). или просто S=(1,2) — нарисовать точку S с координатами (1,2)

Intersect — построить точку пересечения двух прямых, сами прямые нужно строить отдельными командами.

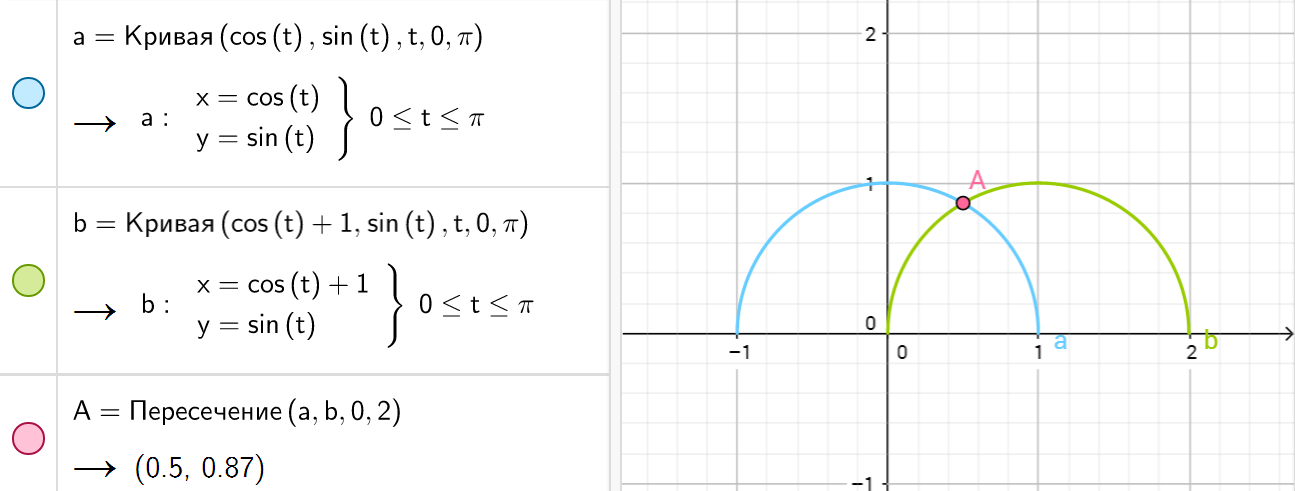
Более сложный пример. Зададим функцию параметрически, введем выражения a = Curve b = Curve и попробуем найти точку пересечения этих кривых a и b на отрезке от 0 до 2: Intersect . Результат:

Символы x, y, z не нужно использовать для именования объектов. Эти имена зарезервированы для получения координат точки. Например: B = (x(T), s) — построить точку B с абсциссой, совпадающей с абсциссой точки T С = (5, y(T)) — построить точку С с абсциссой 5 и ординатой, совпадающей с ординатой точки T.

Команда для получения длины отрезка: Расстояние

Команда для нахождения середины отрезка или центра коники: C=Середина(A,B) Команды: Midpoint, Length, Distance

Последние два инструмента для нахождения корней и точек экстремума выбранной функции:

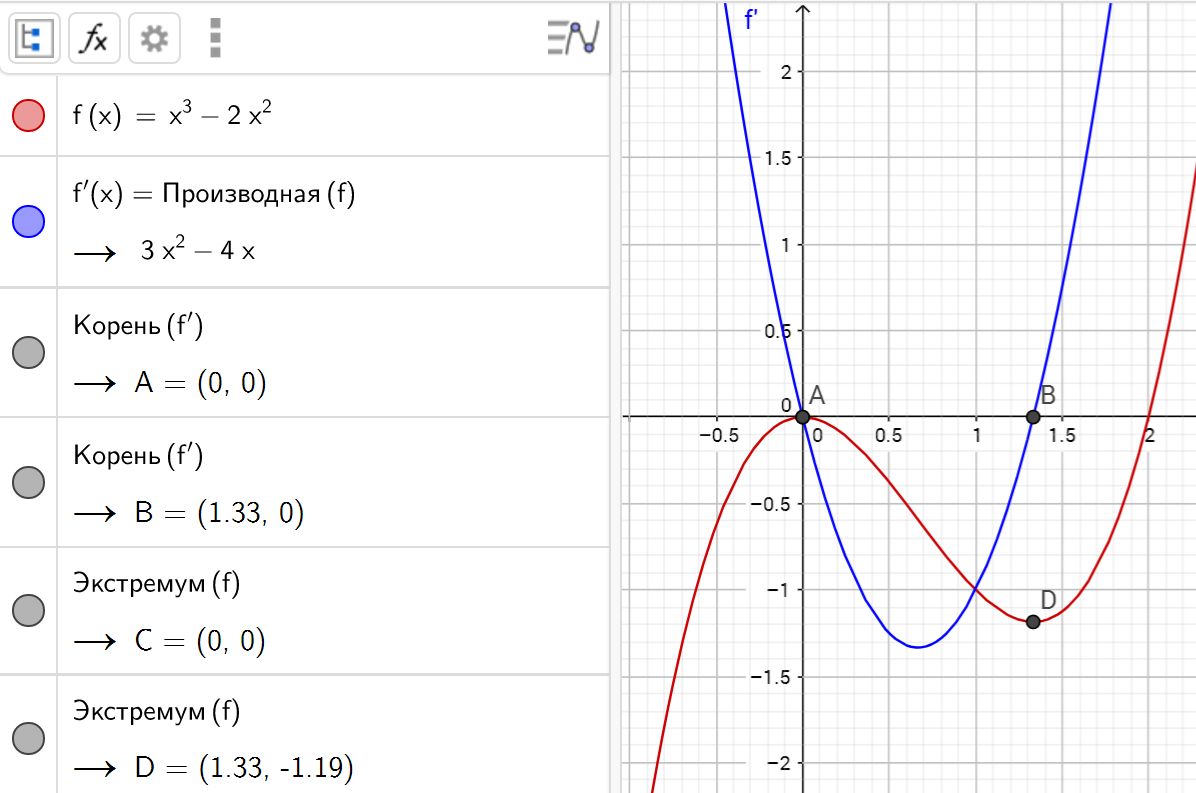
Команды:

Перпендикулярная прямая, биссектриса, касательная

Инструмент Аппроксимация позволяет построить линейную регрессию по набору точек. Пример: FitLine[] результатом будет прямая y=0.4x+2 Синонимы ЛинейнаяАппроксимацияПоX, ЛинейнаяАппроксимацияПоY

Угол, наклон прямой, периметр, площадь

— Построение угла по трем точкам или двум прямым (указывать в порядке против часовой стрелки), угла заданной величины. — Расстояние между двумя точками, длина отрезка, периметр многоугольника, длина окружности или замкнутой кривой. — Площадь многоугольника, окружности или коники. — Наклон прямой (угловой коэффициент) — Создать список — щелкнуть по элементам, затем снова щелкнуть по иконке инструмента

Отношение объектов Инструмент позволяет выбрать два объекта и получить сообщение о равенстве некоторых величин этих объектов. * две прямые перпендикулярны? * две прямые параллельны? * два объекта равны? * прямая является касательной или секущей к конике? * точка лежит на прямой или конике?

Исследователь функции

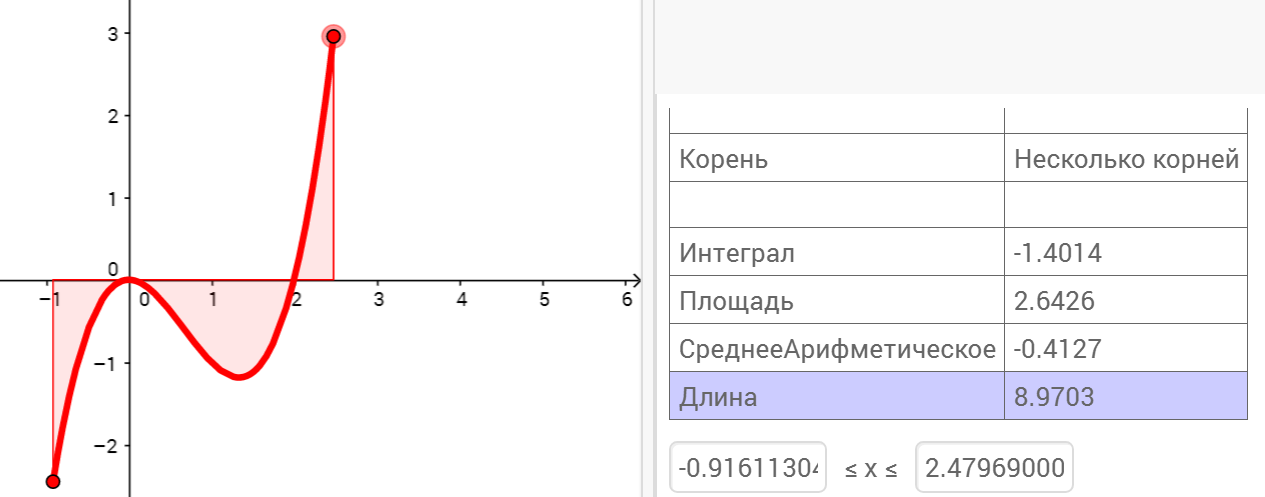
Команды: Угол, Повернуть, Расстояние, Периметр, Периферия, Наклон. Список обозначается фигурными скобками

Отражение, поворот, гомотетия

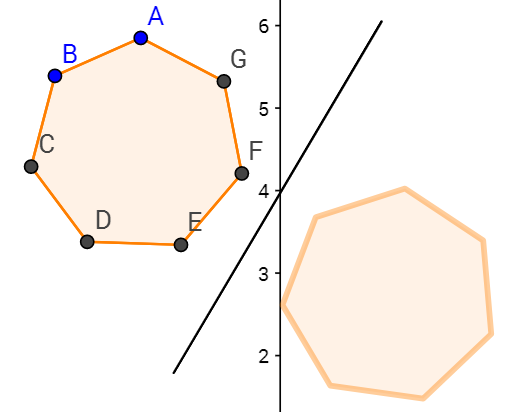
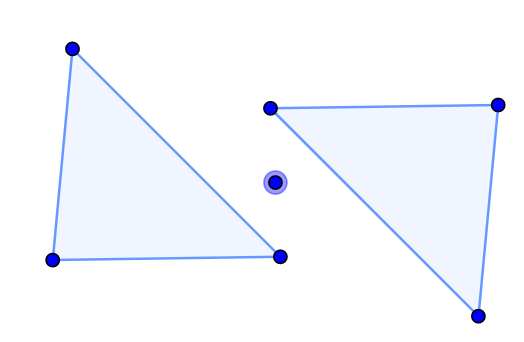
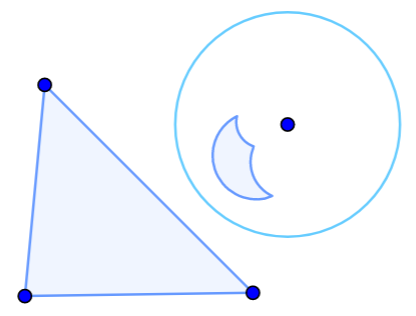
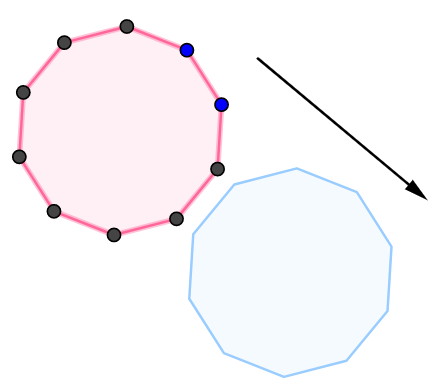
Гомотетия относительно точки: указать проектируемый объект, центр и коэффициент гомотетии.

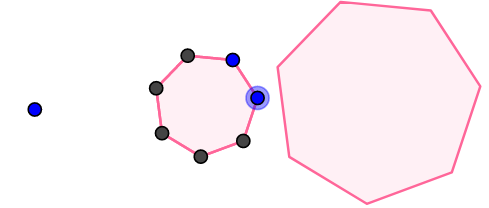
Команды: Отразить, Повернуть, Перенести, Гомотетия

Ползунок, текст и другие элементы

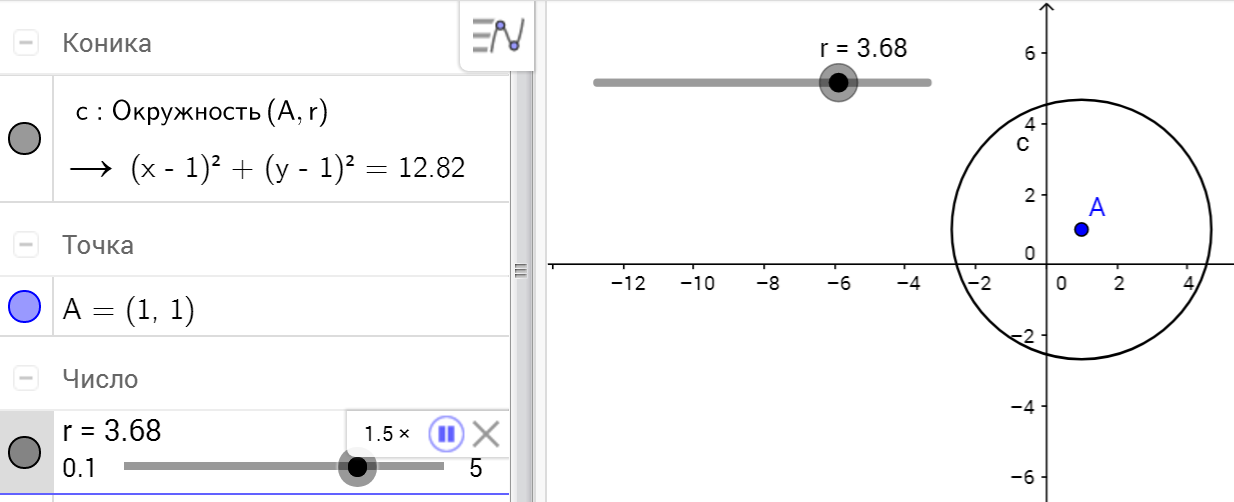
Ползунок (слайдер)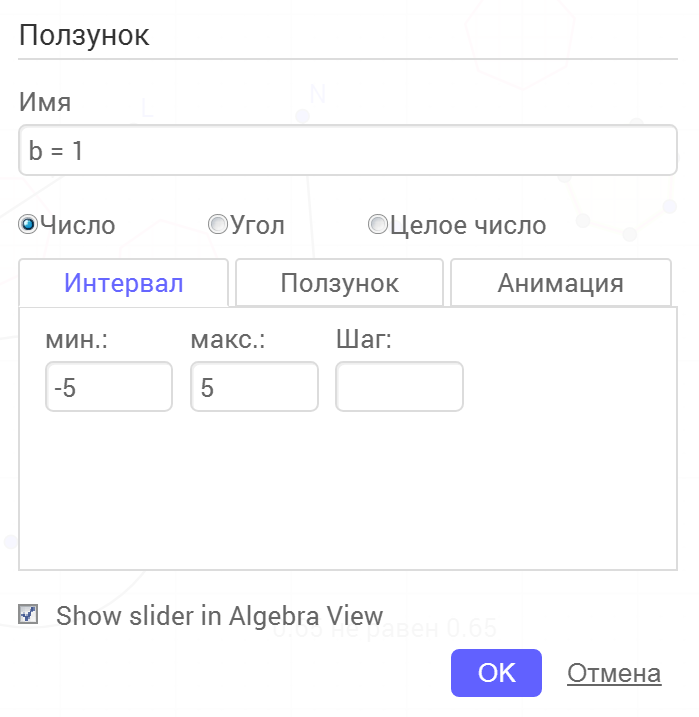

Будет создана точка A, ползунок r и окружность с центром в точке A и радиусом r, который можно менять вручную или включить анимацию.

Изображение

Добавить на чертеж картинку из файла. Можно регулировать прозрачность. Можно сделать фоновым — тогда сетка просвечивает через рисунок.

Текст — создание надписи, пояснительного текста. Поддерживается latex. Надпись можно привязать к определенной точке на чертеже или к месту на листе, абсолютно или относительно — см. свойства. Для создания динамического текста, который будет отображать изменение параметров объекта, выберите объект из списка объектов. Имя объекта в поле ввода заключается в рамку, на чертеже будет показано значение объекта (например, для отрезка будет показана его длина). Правый клик по рамке позволяет переключаться между определением и значением объекта. Если перетащить объект из панели объектов на полотно, надпись будет создана автоматически.

Можно выполнять алгебраические операции или применять команды к объектам, просто вписывая команды в текст. Результат операций будет динамически показан на чертеже. Пример. Ввести команды:

a=10 b=30 c=a+b

Объекты a и b будут преобразованы в ползунки. Перетащите последний объект на чертеж — будет создана надпись. По мере изменения параметров a и b с помощью ползунков сумма этих объектов будет автоматически отображаться на чертеже.

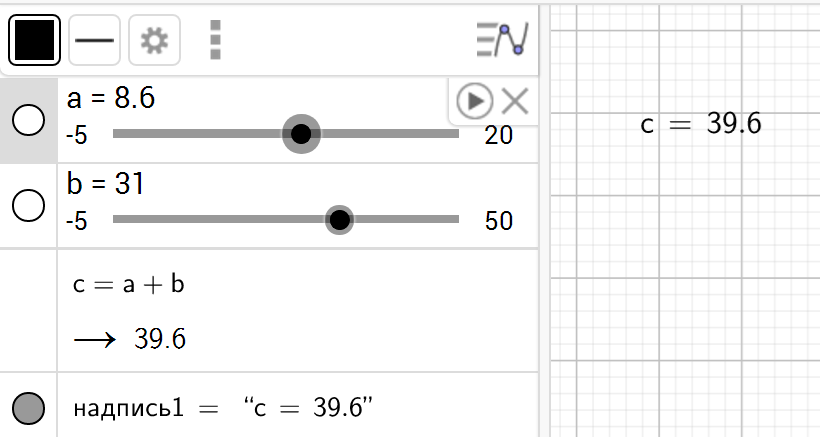
Команды: LaTeX, двойные кавычки

Доступны также такие элементы, как кнопка, флажок, окно ввода.

Масштаб, перемещение полотна, скрытие объекта

Копировать стиль — выбрать объект-источник стиля и объект, к которому следует применить стиль.

Видео:Откладывание вектора от данной точки | Геометрия 7-9 класс #78 | ИнфоурокСкачать

Пример 1: Окружность, описанная около треугольника

Построение с помощью мыши

Меню «Вид — Протокол построения» выводит таблицу, с перечислением всех шагов, которые вы совершили при построении. Это позволяет вам сделать заново построение шаг за шагом при помощи клавиш со стрелками, а также изменить порядок различных шагов (см. меню «Помощь» протокола построения).

Построение с помощью поля ввода текста

Создадим новое окно и введем следующие команды, нажимая ENTER после каждой строки:

Клик по иконке «Ввод» (внизу слева) активирует режим «Поле ввода». В этом режиме вы можете нажать на объект в алгебраическом или графическом окне, чтобы скопировать его имя в поле ввода текста.

Наилучшие результаты вы получите, объединив преимущества обоих способов ввода: с помощью мыши и поля ввода текста.

Видео:Координаты вектора. 9 класс.Скачать

Примеры использования геогебры для построения трехмерных поверхностей

Вот несколько примеров того, как геогебра может использоваться для построения трехмерных поверхностей:

Пример 1: Построение графика функции Геогебра позволяет пользователю ввести уравнение функции и построить ее график в трехмерной системе координат. Например, можно построить график функции y = x^2 + y^2, который представляет собой параболоид. Пользователь может исследовать различные значения функции и наблюдать, как график изменяется при изменении параметров.	Пример 2: Построение поверхности по данным точкам Геогебра позволяет пользователю ввести набор точек в трехмерной системе координат и построить поверхность, проходящую через эти точки. Например, можно построить поверхность, проходящую через вершины параллелограмма. Пользователь может исследовать поверхность, изменять положение точек и наблюдать, как это влияет на форму и структуру поверхности.
Пример 3: Построение трехмерной геометрии Геогебра позволяет пользователю построить трехмерные геометрические фигуры, такие как куб, пирамида, цилиндр и т.д. Например, можно построить куб и вычислить его объем и площадь поверхности. Пользователь может исследовать эти характеристики, изменять размеры фигуры и наблюдать, как это влияет на их значения.	Пример 4: Построение математических функций Геогебра позволяет пользователю строить математические функции в трехмерном пространстве. Например, можно построить функцию z = sin(x) + cos(y), которая представляет собой волнообразную поверхность. Пользователь может исследовать различные значения функции и наблюдать, как поверхность изменяется в зависимости от этих значений.

Это только некоторые примеры использования геогебры для построения трехмерных поверхностей. Возможности геогебры очень широки, и пользователь может экспериментировать с различными математическими концепциями, чтобы получить интересные и визуально привлекательные трехмерные модели и поверхности.

Exercises

The main feature of GeoGebra is not to use it as a tool for making pictures, but rather to use it as a tool for making dynamic constructions. In order to learn GeoGebra however, it may be a good idea to start by making pictures.

Exercise 1

Create, change and delete objects

Check out how to create objects. Make sure you know how to create following objects:

• Circles in two different ways; use the tools Circle with Center through Point and Circle with Center and Radius.
• Polygons in two different ways; use the tools Polygon and Regular Polygon.
• Perpendicular and parallel lines.
• Reflections in lines.
• Intersection points.

Also make sure you know how to:

• change the appearance of the objects you created and how to move them around,
• change the appearance of the graphics view,
• show text in the graphics view.

Also try to:

• regret by clicking ctrl+z or cmd+z, or by using the icons in the upper right corner of the GeoGebra window,
• zoom in and out using the mouse wheel or trackpad.

Exercise 2

Make a self portrait

When you are done, hide all objects that shouldn’t be visible. Under the advanced tab in the properties window, you can choose a Layer for an object. Using layers, objects can be drawn «above» other objects.

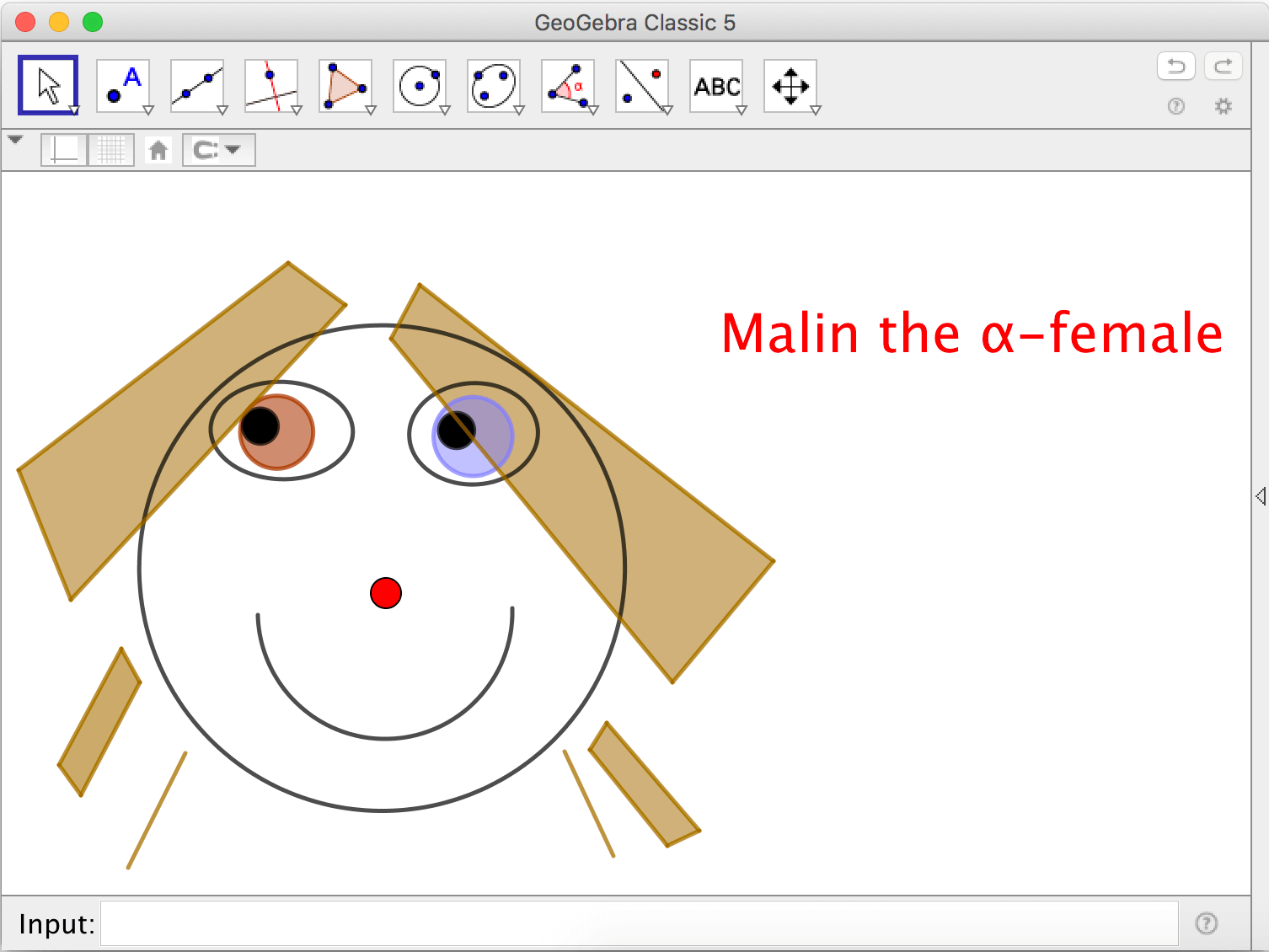
Exercise 3

Make a symmetric self portrait

In order to make a symmetric portrait; make half of the face on one side of the y-axis, then use the tool Reflect about line, using the y-axis as line of symmetry.

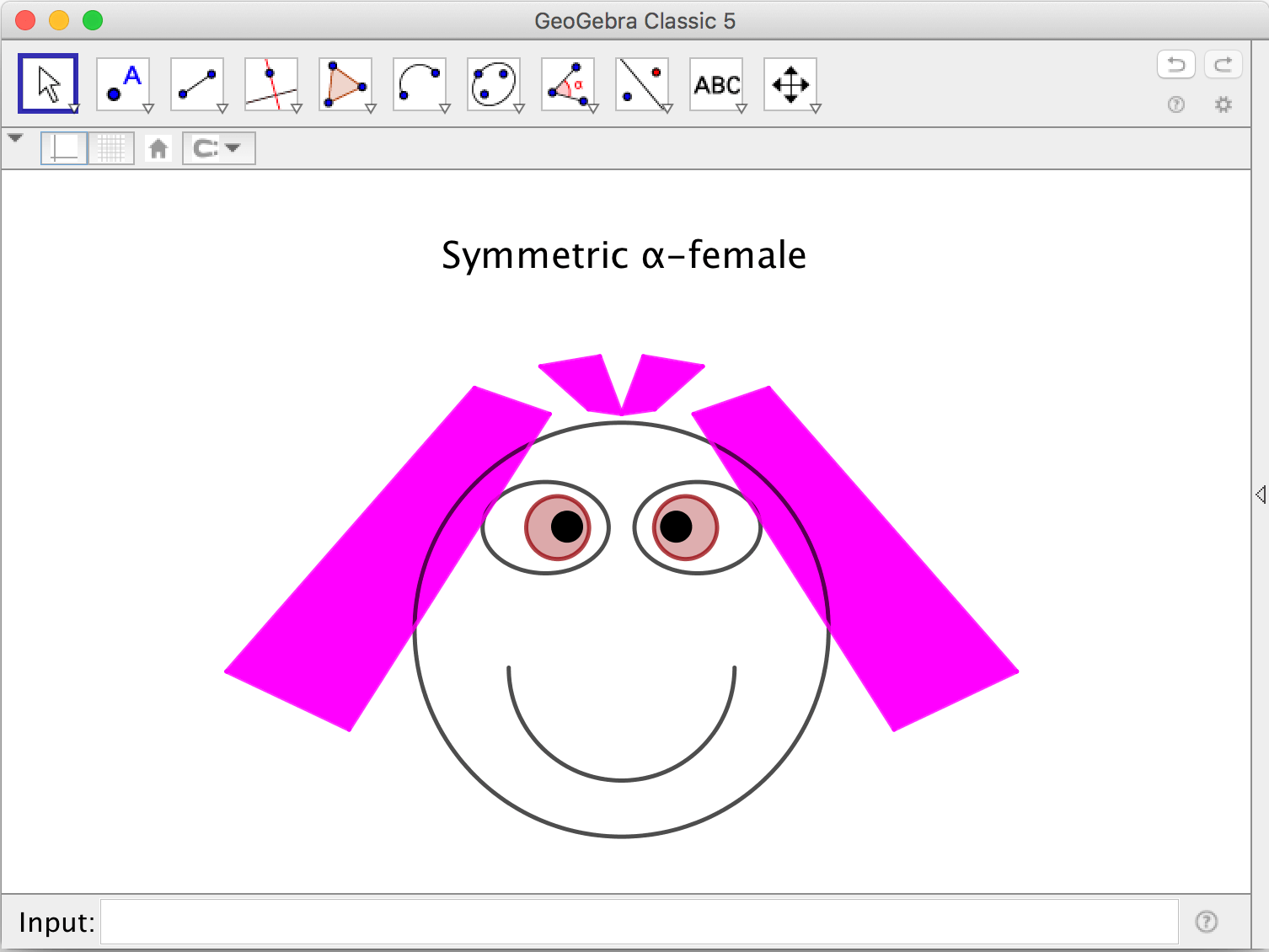
Exercise 4

Sliders

• Make a slider a using the tool Slider and a circle having a as radius. Use the tool Circle with Center and Radius.
• Make a slider n of integer values and make a Regular Polygon having n vertices.
• Make a slider \(\alpha\) representing an angle. Make a polygon and a point not on the polygon. Use the tool Rotate around point to rotate the polygon around the point \(\alpha\) degrees.

Знакомство с функциональностью геогебры для построения трехмерных моделей

Для начала работы с трехмерными моделями в геогебре необходимо открыть приложение и создать новый документ. После этого можно приступить к построению трехмерных объектов.

Главным элементом в геогебре для построения трехмерных моделей является команда «Построить». При щелчке на эту команду открывается меню с различными опциями построения. В этом меню можно выбрать различные объекты, такие как точки, линии, поверхности и многое другое.

После выбора нужного объекта, необходимо указать его параметры и положение в пространстве. Настройки параметров можно осуществить через диалоговое окно, которое открывается после выбора объекта.

Одной из самых полезных функций геогебры для построения трехмерных моделей является возможность задать уравнение поверхности. Для этого необходимо выбрать соответствующую команду в меню «Построить» и ввести уравнение.

Кроме того, в геогебре есть возможность добавить различные элементы в модель, такие как оси координат, маркеры и инструменты измерения. Это помогает визуализировать трехмерные объекты и улучшить их понимание.

Геогебра также предоставляет возможность вращать и масштабировать трехмерные модели, чтобы рассмотреть их с разных ракурсов. Для этого нужно просто использовать специальные инструменты в интерфейсе программы.

GeoGebra

О программе

GeoGebra – это бесплатная, кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику, в одном удобном для использования пакете.

Основные возможности

Построение кривых:

1. Построение графиков функций y=f(x)
2. Построение кривых, заданных параметрически в декартовой системе координат: x=f(t); y=g(t)
3. Построение конических сечений (окружность, эллипс, парабола, гипербола)
4. Построение геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику

Вычисления:

1. Действия с матрицами (сложение, умножение, транспонирование, вычисление определителя)
2. Вычисления с комплексными числами
3. Нахождение точек пересечения прямых
4. Статистические функции (вычисление математического ожидания, дисперсии, коэффициента корреляции)
5. Аппроксимация множества точек кривой заданного вида (полином, экспонента, логарифм, синусоида)

Решение задач алгебры

1. Найти корни квадратного уравнения x^2+3x-4=0 на промежутке от -10 до 10

Алгоритм решения:

1. Ввести функцию f(x)=x^2+3x-4
2. Воспользоваться командой

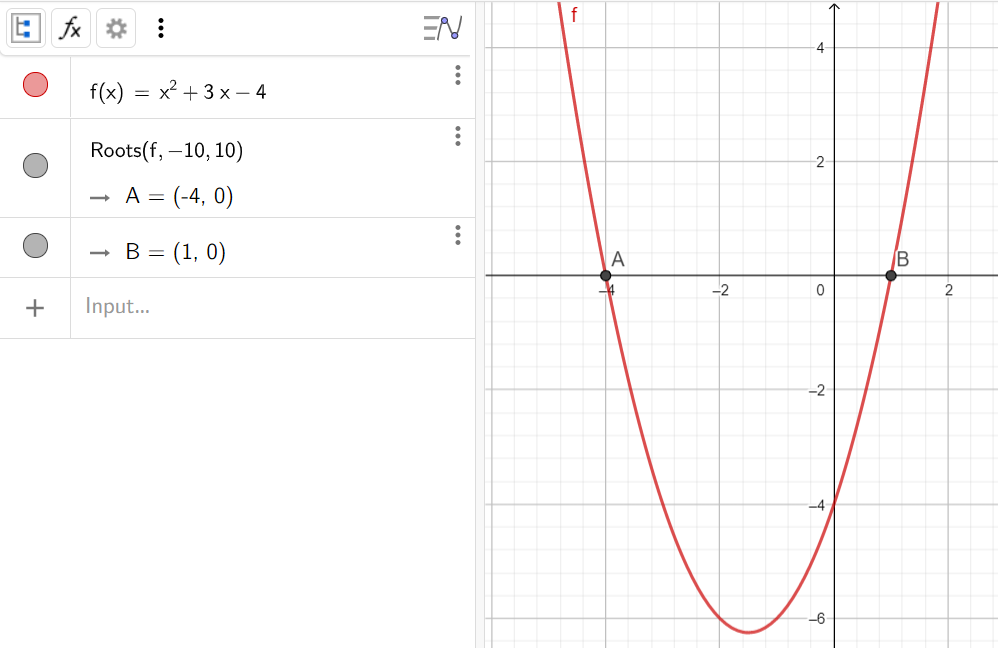
2. Найти корни тригонометрического уравнения sin⁡(x)+cos⁡(x)=1 на промежутке от -2π до 2π

Алгоритм решения:

1. 3. Преобразовать выражение: sin⁡(x)+cos⁡(x)-1=0
2. Ввести функцию f(x)=sin⁡(x)+cos⁡(x)-1
3. Воспользоваться командой

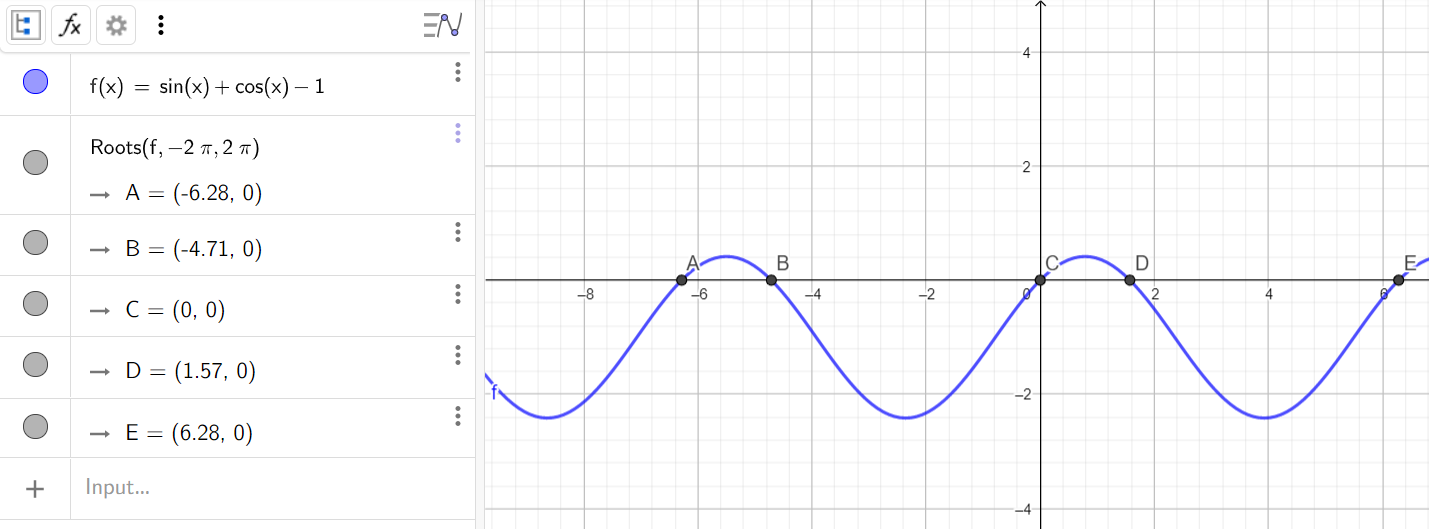
Разделить один многочлен x^2+3x+1 на другой x-1

Синтаксис:

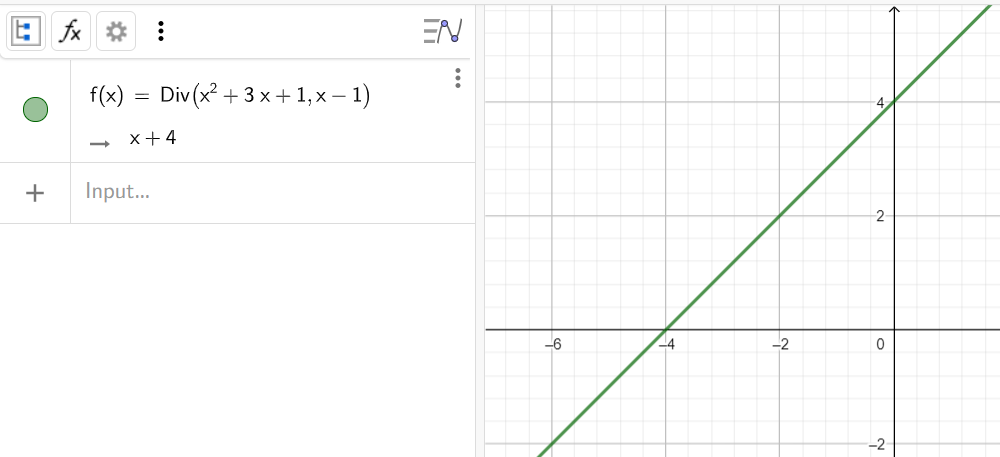
4. Упростить выражение (2x-1)^2+2x+3

Синтаксис:

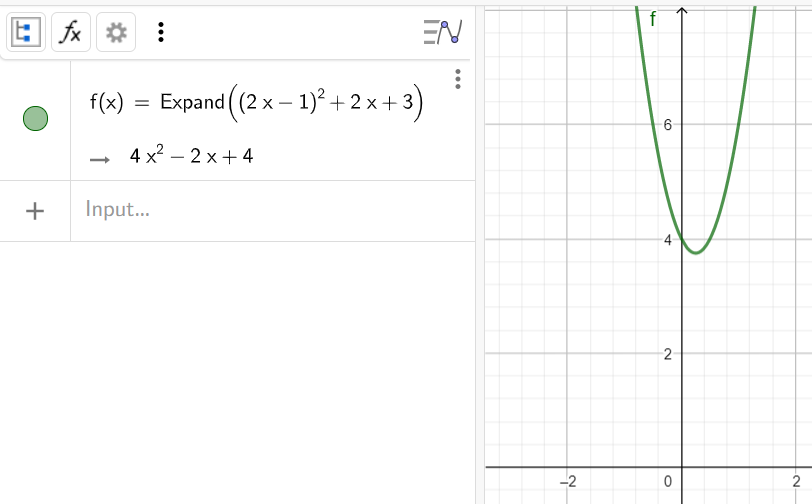
5. Разложить на множители многочлен x^2+x-6

Синтаксис:

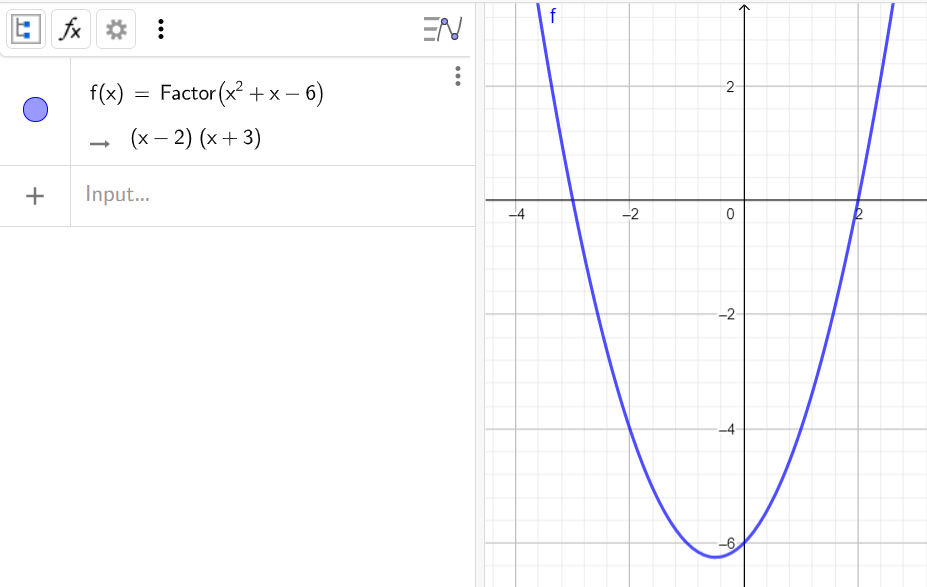
6. Найти наибольший общий делитель чисел 12, 30, 18

Синтаксис:

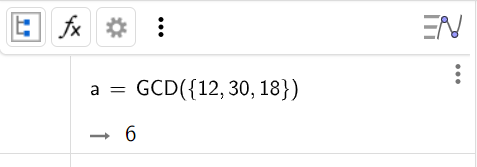
7. Найти наименьшее общее кратное чисел 12, 30, 18

Синтаксис:

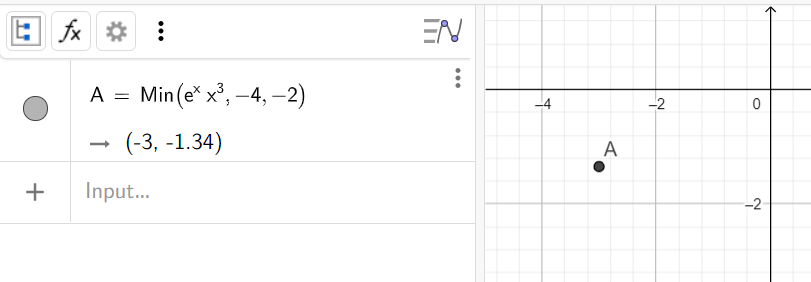
8. Найти наименьшее значение функции e^x*x^3 на промежутке от -4 до -2

Синтаксис:

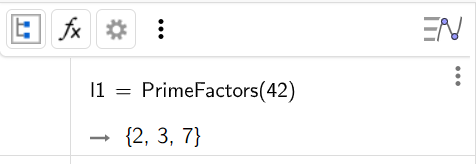
9. Разложить число 42 на простые множители

Синтаксис:

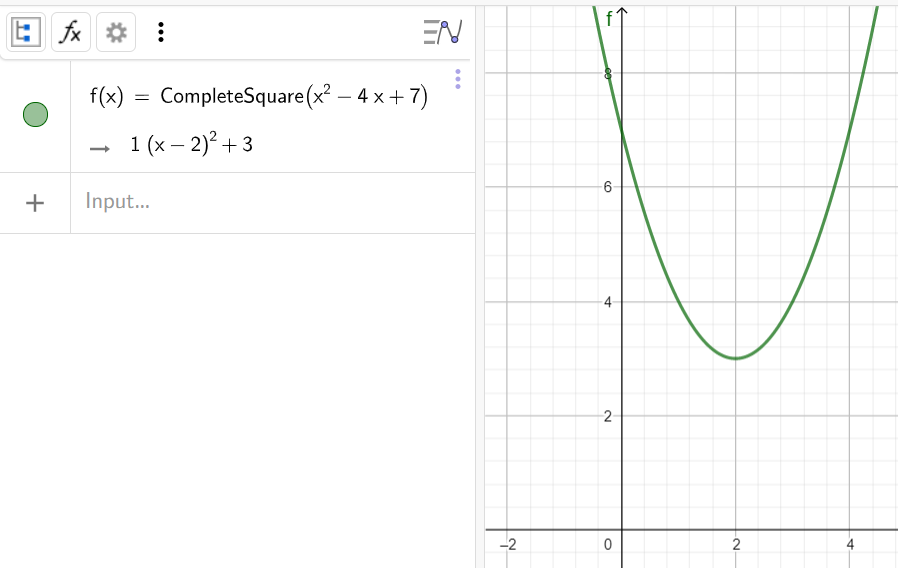
10. Выделить полный квадрат x^2-4x+7

Синтаксис:

11. Найти декартово произведение векторов A{1,3,2} и B{0,3,-2}

Синтаксис:

12. Найти определитель матрицы

Синтаксис:

Решение задач математического анализа

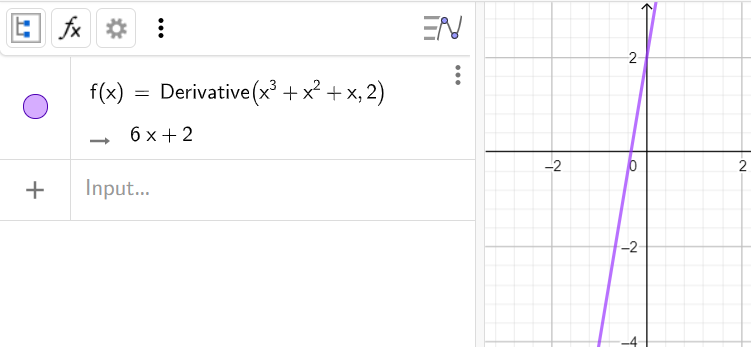
1. Найти первую производную функции x^3+x^2+x

Синтаксис:

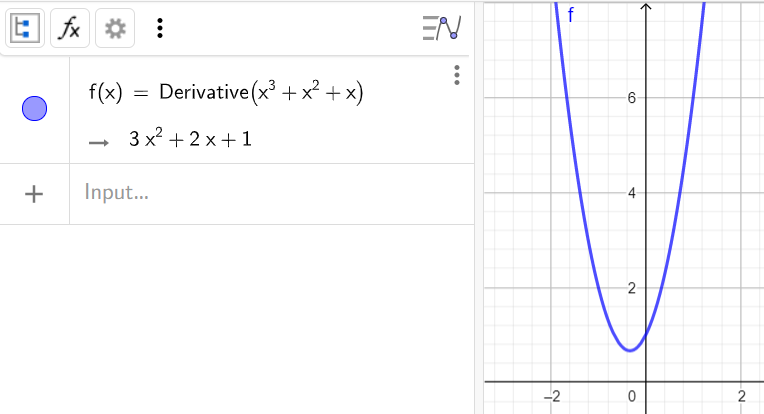
2. Найти вторую производную функции x^3+x^2+x

Синтаксис:

3. Найти экстремум функции

Синтаксис:

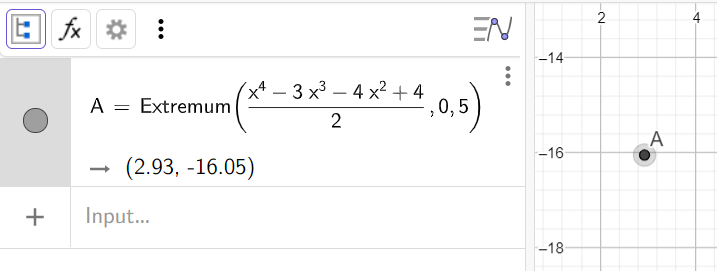
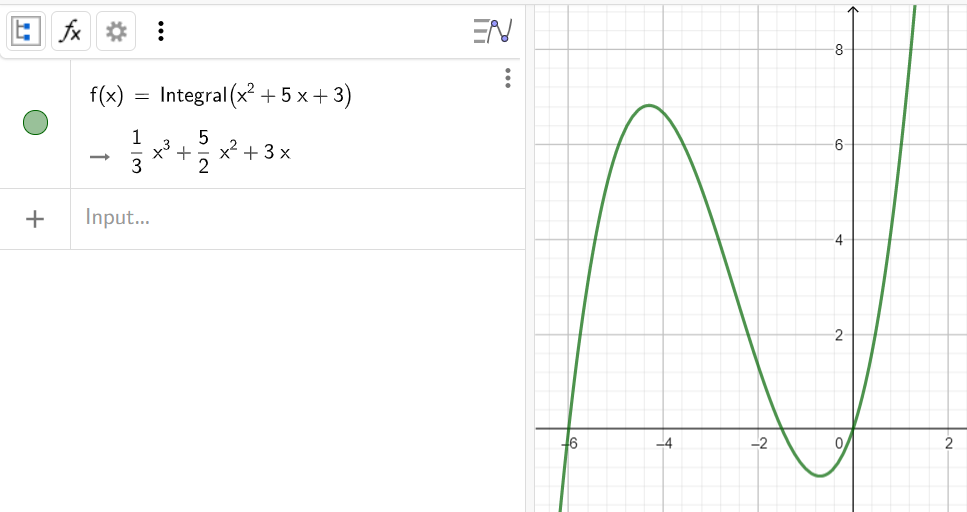
4. Вычислить неопределенный интеграл ∫(x^2+5x+3)dx

Синтаксис:

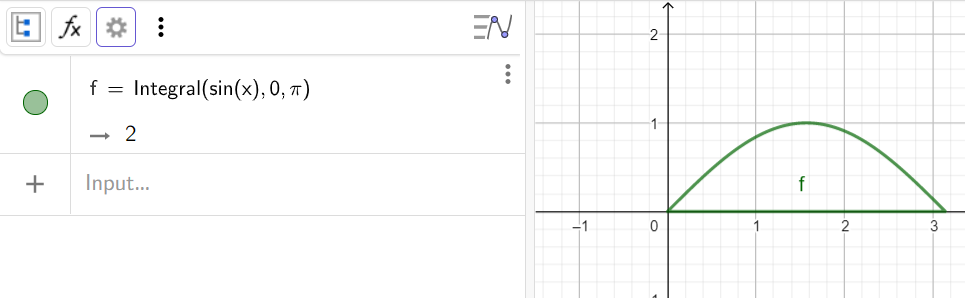
5. Вычислить определенный интеграл

Синтаксис:

6. Найти предел

Синтаксис:

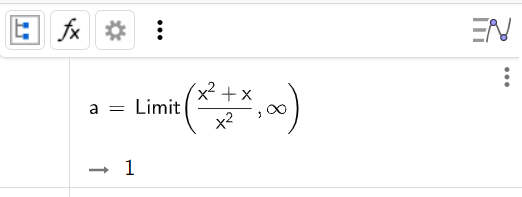
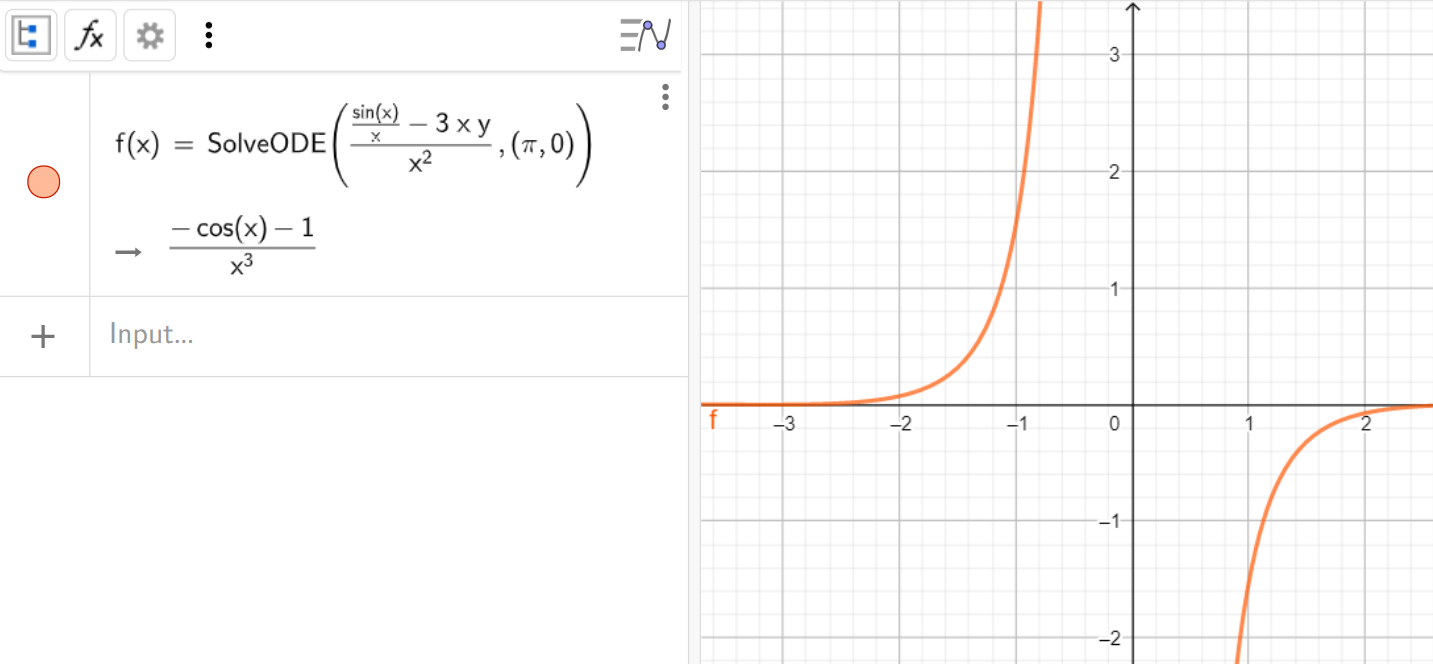
7. Решить дифференциальное уравнение первого порядка при

Алгоритм решения:

1. Преобразовать выражение:
2. Воспользоваться командой

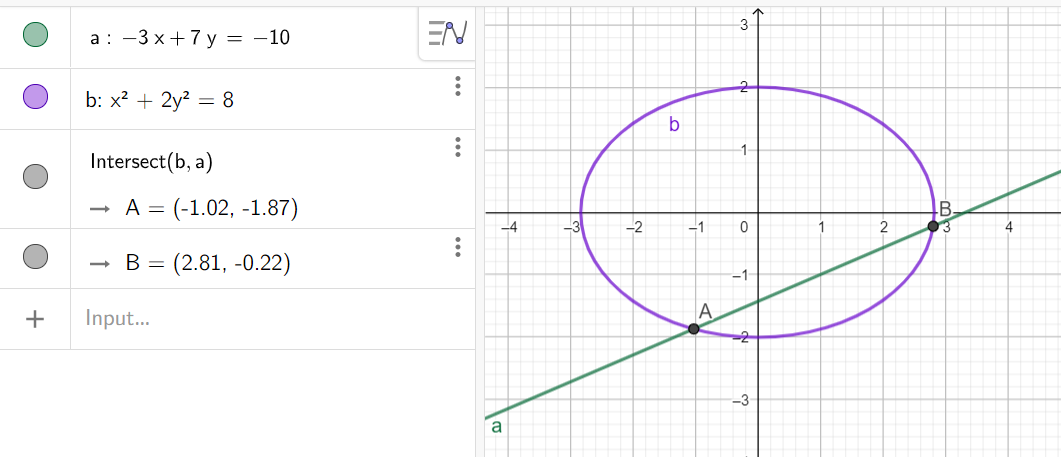
Решение задач геометрии

1. Найти точки пересечения -3x + 7y = -10 и x^2 + 2y^2 = 8

Алгоритм решения:

1. Ввести a: -3x + 7y = -10
2. Ввести b: x^2 + 2y^2 = 8
3. Воспользоваться командой
   В данном случае:

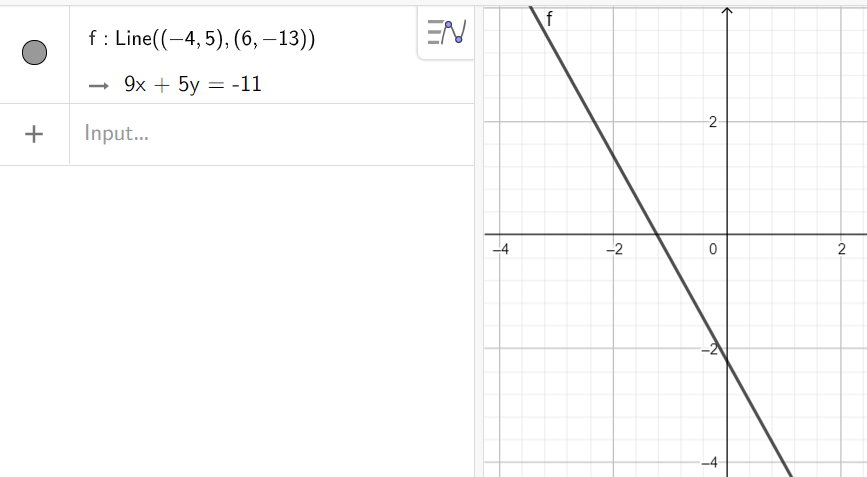
2. Построить линию через две точки A(-4,5) и B(6,-13)

Синтаксис:

3. Найти периметр многоугольника с координатами A(1,2),B(3,2) и C(4,3)

4. Построить правильный шестиугольник по двум заданным точкам A(1,1),B(4,1)

Синтаксис:

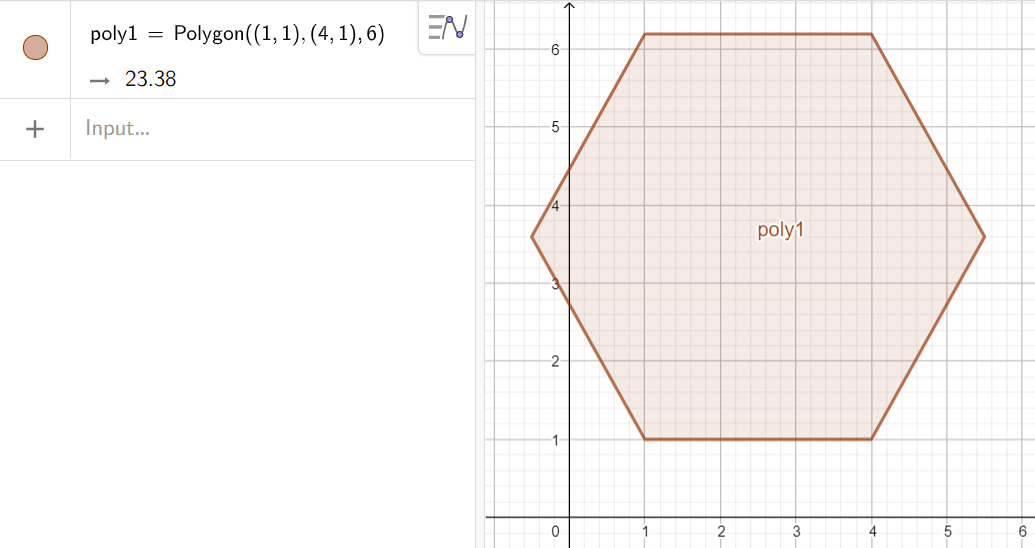
5. Найти радиус окружности, заданной уравнением (x — 2)² + (y — 2)² = 24

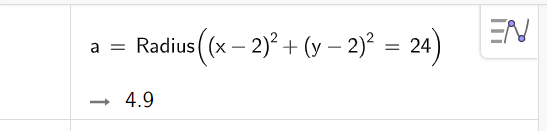
6. Найти расстояние между двумя прямыми y = x + 3 и y = x + 1

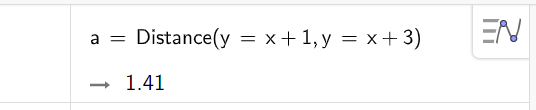
7. Найти расстояние между точкой A(2,1) и объектом, заданным уравнением x^2 + (y — 1)^2 = 1

Синтаксис:

Программа по математике GeoGebra — инструкция как с ней работать

Возникали ли у вас необходимость построить график функции? Поможет бесплатная программа по математике GeoGebra. Она анализирует функции, решает задачи, строит графики. Рассмотрим подробно, как установить, скачать и работать с этой программой.

Что это такое

GeoGebra — программа по математике. Написана на языке программирования Java. Разработана Маркусом Хохенвартером. Приложение не ограничивается только работой с графиками. Используйте ее для создания чертежей, решении задач по геометрии, разработке анимации.

Решает такие задачи:

1. Обучение алгебре и геометрии;
2. Создание графиков и таблиц;
3. Работа со статическими данными;
4. Анимация;
5. Создание 2D, 3D фигур;
6. Создание интерактивных роликов с последующим размещением в интернет.

• сохраните форматом GeoGebra;
• распечатайте;
• экспортируйте в форматах SVG, PNG, PDF.

По адресу: https://wiki.geogebra.org/ru/Руководство находится руководство пользователя, с информацией про работу с объектами.

Как скачать

1. Graphing Calculator. Используйте ее для решения уравнений, нахождение специальных функций, возможность поделиться результатами с другими людьми;
2. Geometry. Для создания геометрических фигур, рисования.

1. Скачать приложения для ОС Windows, Mac бесплатно на русском.
2. Установить расширения в браузер Chrome,
3. Загрузить приложения для работы на смартфонах и планшетах.

Скачиваем инсталляционный «exe» файл. Нажимаем по нему мышкой два раза для начала загрузки. Установка простая, не вызовет сложностей даже у начинающий пользователей.

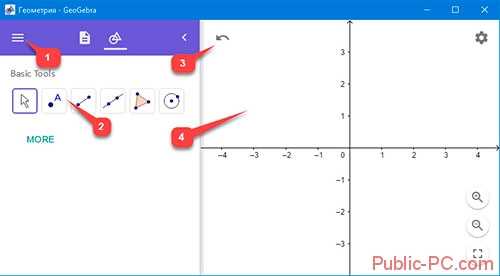
Интерфейс

Напоминает графический редактор. Рассмотрим его основные элементы:

1. Кнопка меню (три горизонтальные линии). Используйте для изменения настроек;
2. Панель инструментов. Для создания фигур и графиков;
3. Стрелки отменяющие действия;
4. Рабочая область. Все действия происходят в ней. При помощи колеса мыши редактируйте масштаб.

Чтобы настроить приложение для работы, сделайте следующее. Нажимаем кнопку настроек (три горизонтальные линии)-«Apps». Выбираем необходимое: калькулятор, геометрия, 3D. Рассмотрим некоторые возможности программы.

Как построить график

Выбираем в настройках «Apps»-«Графический калькулятор». Действия происходят в поле ввода. Например, построим параболу. Прописываем: x^2. Или используйте кнопки внизу программы. Нажимаем «Enter». На рабочей области построится график.

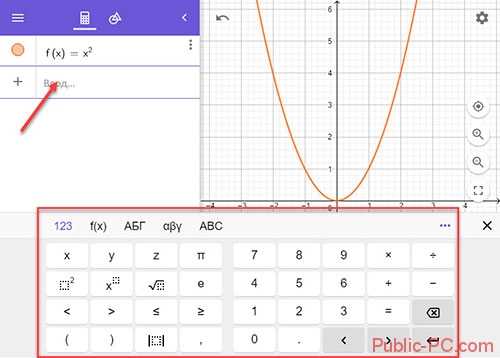Добавляйте переменные. Пропишите их в строку формулы.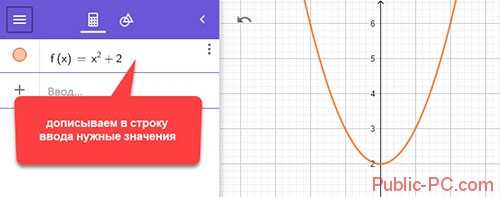

Как создать 3D

В настройках переходим «Apps»-«3D». Выбираем инструменты кликнув по иконке. Далее постройте объект следуя подсказкам. 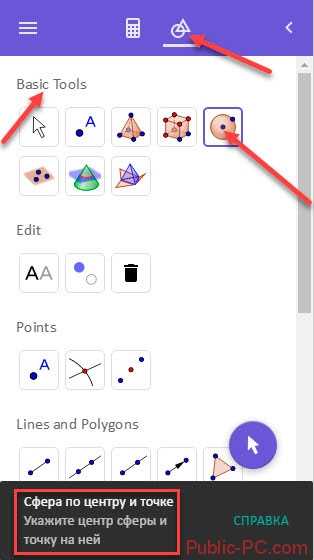Выполняем нужные действия.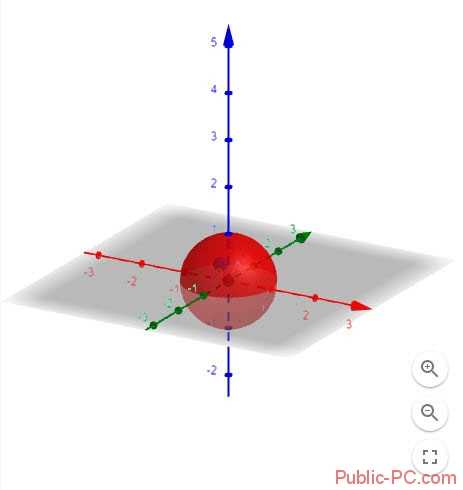

GeoGebra online на русском

Не хотите загружать дополнительный софт? Используйте онлайн (online) версию, расположенную по адресу: https://www.geogebra.org/classic . Единственное условие необходимое для работы — наличие интернет.

GeoGebra с широким функционалом, предназначена для обучения алгебре и геометрии. Если не удалось установить ее на ПК, используйте online версию. Мне кажется она удобнее. Остались вопросы, инструкция по работе с GeoGebra поможет разобраться детальнее.

Начало работы с геогеброй: основные инструменты

1. Инструмент «Точка»

Инструмент «Точка» позволяет создавать точки на координатной плоскости или на поверхности. Чтобы создать точку, просто кликните на нужном месте в окне геогебры. Вы можете задать точке имя и изменить ее координаты. Точка будет отображаться на графике и может использоваться в дальнейших вычислениях.

2. Инструмент «Отрезок»

Инструмент «Отрезок» позволяет строить отрезки между двумя точками на координатной плоскости или на поверхности. Чтобы построить отрезок, выберите инструмент «Отрезок», затем кликните на одну точку и затем на другую. Вы можете задать отрезку имя и изменить его длину или угол.

3. Инструмент «График»

Инструмент «График» позволяет строить графики функций на координатной плоскости. Чтобы построить график, выберите инструмент «График», затем введите уравнение функции в соответствующее поле. Геогебра автоматически построит график функции и покажет его на экране. Вы можете изменить параметры функции и построить несколько графиков на одном графическом окне.

4. Инструмент «Поверхность»

Инструмент «Поверхность» позволяет строить трехмерные поверхности. Чтобы построить поверхность, выберите инструмент «Поверхность», затем введите уравнение поверхности в соответствующее поле. Геогебра автоматически построит поверхность и отобразит ее на экране. Вы можете изменить параметры поверхности и построить несколько поверхностей на одном 3D-окне.

Это лишь небольшой список основных инструментов геогебры. В дальнейшем вы можете изучить и использовать более сложные инструменты, такие как инструмент «Угол», инструмент «Параллельные линии» и многое другое

Важно начать с основных инструментов и постепенно углублять свои знания и навыки в работе с геогеброй

Для чего предназначена программа GeoGebra 6.0.450

GeoGebra – это математическое ПО, разработанное для различных образовательных учреждений. Программа написана на языке Java, поэтому для её корректной работы потребуется скачать и установить пакет от Java.

Инструменты для работы с математическими объектами и выражениями

GeoGebra предоставляет широкие возможности для работы с геометрическими фигурами, алгебраическими выражениями, таблицами, графами, статистическими данными и арифметикой. Все функции включены в один пакет для удобства. Также есть средства для работы с различными функциями, например, графиками, корнями, интегралами и т.д.

Конструирование стереометрических чертежей

В данной программе предусмотрена возможность работать в 2-х и 3-х мерном пространстве. В зависимости от выбранного пространства для работы, вы получите двумерную или трёхмерную фигуру соответственно.

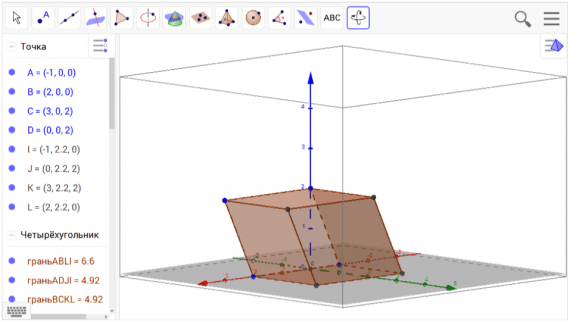
Геометрические объекты в GeoGebra формируются при помощи точек. Каждой из них можно задать те или иные параметры, провести через них линию. С готовыми фигурами тоже можно производить различные манипуляции, например, отмечать на них углы, производить измерение длины линий и сечения углов. Через них также можно проложить сечения.

Независимое построение объектов

В GeoGebra есть также функция выноса рисунка, которая позволяет делать построение объектов отдельно от основной фигуры. Например, вы можете построить какой-нибудь многогранник, а отдельно от него вынести какой-либо его компонент – угол, линию или несколько линий и углов. Благодаря этой функции можно наглядно показывать и рассказывать об особенностях какой-либо фигуры или её части.

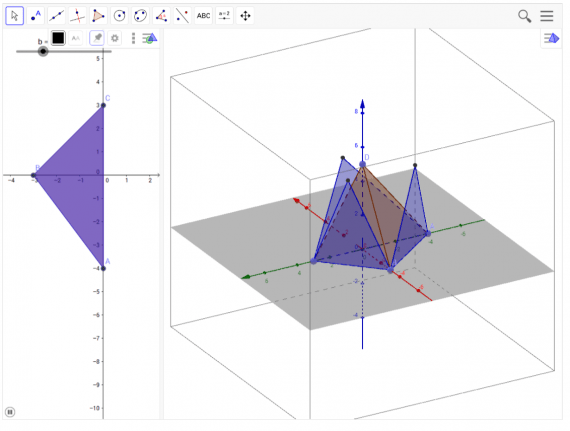
Построение графиков функции

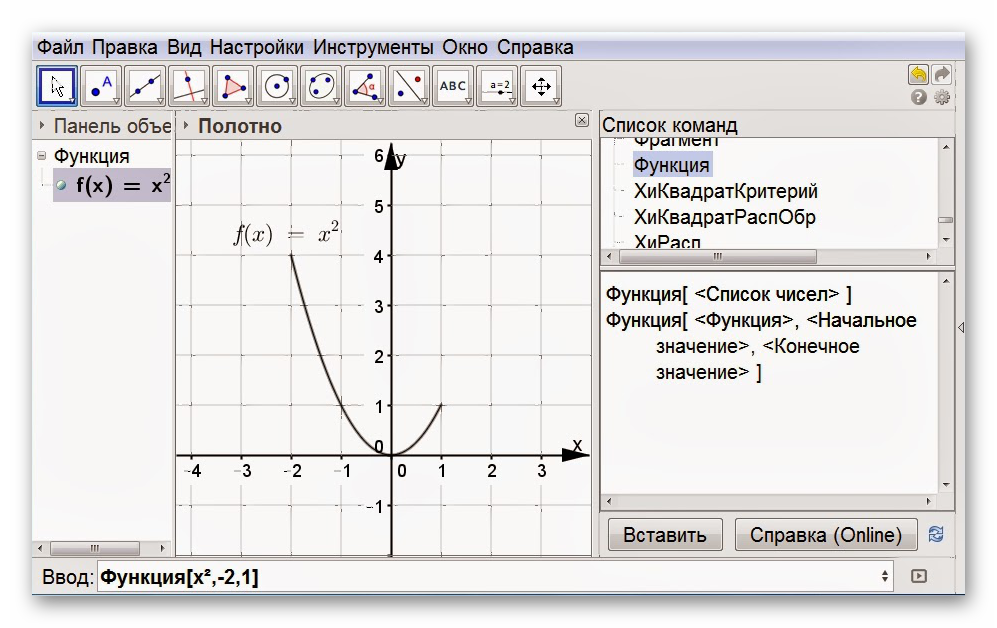
В ПО встроен функционал, необходимый для создания различных графиков функций. Для управления ими можно использовать как специальные ползунки, так и прописывать определённые формулы. Вот простой пример:

Возобновление работы и поддержка сторонних проектов

В программе можно возобновить работу с проектом после закрытия. При необходимости можно открывать проекты, которые были скачаны с интернета и вносить туда свои корректировки.

Сообщество GeoGebra

На данный момент программа активно разрабатывается и совершенствуется. Разработчики создали специальный ресурс – GeoGebra Tube, где пользователи ПО могут делится своими предложениями, рекомендациями, а также уже готовыми проектами. Как и сама программа, все проекты, представленные на данном ресурсе, абсолютно бесплатны и их можно копировать, адаптировать под свои нужды и использовать без каких-либо ограничений в некоммерческих целях.

На данный момент на ресурсе выложено более 300 тысяч проектов и это число постоянно растёт. Единственный недостаток – это то, что большая часть проектов на английском языке. Но нужный проект можно скачать и перевести на ваш язык уже на компьютере.

Достоинства

• Удобный интерфейс, переведённый на русский язык;
• Большой функционал по работе с математическими выражениями;
• Возможность работы с графикой;
• Наличие собственного комьюнити;
• Кроссплатформенность: GeoGebra поддерживается практически всеми известными платформами – Windows, OS X, Linux. Есть приложение для Android и iOS смартфонов/планшетов. Также имеется браузерная версия, доступная в магазине приложений Google Chrome.

Недостатки

• Программа находится на стадии разработки, поэтому иногда могут встречаться баги;
• Многие проекты, которые выкладываются в сообществе, на английском языке.

GeoGebra больше подходит для создания более продвинутых графиков функции, чем те, которые изучаются в стандартном школьном курсе, поэтому школьным учителям лучше поискать более простые аналоги. Однако преподавателям ВУЗов такой вариант придётся очень кстати. Но благодаря своему функционалу программа может быть использована для показа наглядной демонстрации школьникам. Помимо различных фигур, линий, точек и формул, презентацию в данной программе можно разнообразить при помощи картинок стандартных форматов.

Параметры и настройки трехмерных моделей в геогебре

При работе с трехмерными моделями в геогебре, можно настроить различные параметры, чтобы достичь желаемого визуального эффекта. В этом разделе мы рассмотрим основные параметры и настройки, доступные при построении трехмерных моделей в геогебре.

1. Размер и масштаб:

В геогебре вы можете изменить размер и масштаб трехмерной модели, чтобы она соответствовала вашим потребностям. Для этого вам потребуется использовать параметры scale (масштабирование), width (ширина) и height (высота).

2. Цвет и материал:

Геогебра предлагает широкий выбор цветов и материалов для вашей трехмерной модели. Вы можете выбрать цвет для модели в целом, а также для конкретных ее элементов, таких как поверхности, ребра или вершины. Вы также можете выбрать различные материалы для модели, такие как блеск, металлический отблеск или стекло.

3. Отображение точек и осей:

Вы можете включить или выключить отображение точек и осей в трехмерной модели. Это особенно полезно, когда вам нужно сделать модель более наглядной или упростить ее представление.

4. Анимация и вращение:

Геогебра позволяет создавать анимации и вращения трехмерных моделей

Вы можете настроить скорость вращения, направление и другие параметры анимации, чтобы привлечь внимание к особенностям или деталям модели

5. Взаимодействие с моделью:

Вы можете включить взаимодействие с трехмерной моделью, чтобы пользователи могли изменять ее параметры и исследовать различные варианты. Например, вы можете разрешить пользователям изменять размеры фигуры или поворачивать ее вокруг оси.

Параметр	Описание
scale	Масштабирование трехмерной модели
width	Ширина трехмерной модели
height	Высота трехмерной модели
color	Цвет трехмерной модели
material	Материал трехмерной модели
show points	Отображение точек трехмерной модели
show axes	Отображение осей трехмерной модели
rotation	Вращение трехмерной модели
interaction	Взаимодействие с трехмерной моделью

В целом, параметры и настройки трехмерных моделей в геогебре предоставляют множество возможностей для создания интерактивных и визуально привлекательных моделей. Используйте эти возможности, чтобы сделать свои трехмерные модели более выразительными и удобными в использовании.

Интерфейс GeoGebra

Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.

Давайте рассмотрим основные элементы интерфейса программы GeoGebra:

1. Полоса меню. Из меню вы можете изменить настройки программы.
2. Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
3. Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
4. Кнопки «Отменить» и «Повторить».
5. Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
6. Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.

Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra.